Facebook Hacker Cup: A Geometric Approach to Double Squares Problem

Given an integer N, we need to find the number of integral pairs (x, y) such that x^2 + y^2 = N.

n can range from [0, 2147483647] and there can be a max of 100 such numbers in the input file.

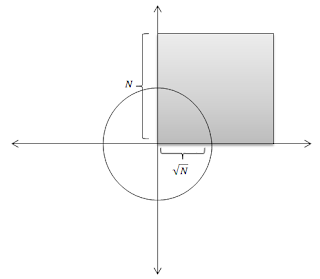
From elementary geometry, we know that x^2 + y^2 = r represents a circle centered at (0,0) with a radius r. Therefore, x^2 + y^2 = n represents a circle with radius n. This is illustrated in figure 1. Now the problem is to find all possible solutions to this equation (in the first quadrant) where x, y are integers.

Figure 1

Bruteforcing all possible integral pairs of (x, y) upto n is equivalent to searching within the geometric space (grey rectangle) illustrated in fig 2.

Figure 2

Algorithmically this approach takes O(n^2) time.Consider the sample input as shown below (this was the file I received)

20

1105

65

2147483646

1257431873

25

1000582589

1148284322

5525

0

1475149141

858320077

1022907856

1041493518

3

1215306625

372654318

160225

5928325

2147483643

1538292481

On my machine, brute force approach takes approx 14 hours (!!!) to solve this input. Obviously Facebook wasnt kidding when it hinted: "Too hard to bruteforce, switching to dp". Clearly, we are exploring a lot of unwanted points. One obvious way to improve this is to explore points bounded by the circle as shown by blue shaded rectangle in fig 3.

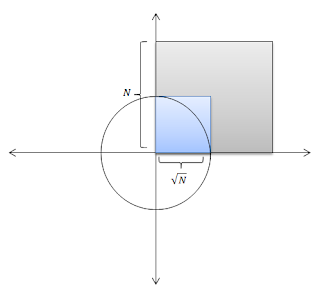
Figure 3

This is equivalent to looping x and y from 0 to n. This makes sense because x or y can never exceed . For example, with n = 25, if x = 5, y = 0 and vice versa. This reduces the complexity from O(n^2) to O(n) reducing execution time from 14 minutes to 80.5 sec!

Can we do any better? Why are we even exploring the blue rectangular region? Its sufficient if we examine all points on the arc of the circle in the first quadrant. i.e., we can increment x = 0 to x' (if x' is irrational number, its safe to use ceil(x')) and examine if the corresponding y points on the circle is an integer. y can be calculated using sqrt(n - x^2). Y is an integer if floor(y) == y. As illustrated in figure 4, all the points to the left of the line y=x is the mirror image of the points to the right. i.e, if we find a point, say (3, 4) to the left of y=x, then we will find a mirror image at (4, 3). Since the problem doesn't differentiate between these two. It is sufficient if we iterate x until the point x'. x' is given by .

Figure 4

With this, the complete algorithm in JAVA is listed below:

private static int getNumSumSquares(int n) 
{
if(n==0)
return 1;

int iterations = (int) Math.ceil(Math.sqrt((n * 1.0)/2));
double y;
int count = 0;
for(int x=0; x <= iterations; x++)
{
y = Math.sqrt(n - (x*x));
//check if y = int.
if(Math.floor(y) == y)
count++;
}
return count;
}

This algorithm works in O(sqrt(n/2)) ~ O(sqrt(n)). This is a huge improvement over the naive approach. With these improvements, it just takes 0.047 secs to execute!